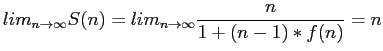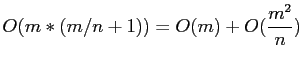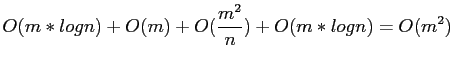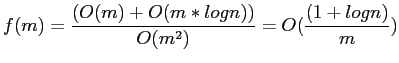Amdahl's Law
A simple algorithm to perform such computation consists of the following three steps:
- The root node sends the vector
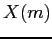 to all processors in the order of
to all processors in the order of
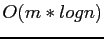
- All processors perform the product
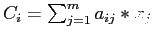 in
in
- All processors send their
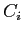 values to the root node in
values to the root node in
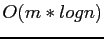 .
.
- According to the above algorithm, the amount of computation needed is
- The indivisible part of the computation is equal to
- Therefore, the fraction of computation that is indivisible
- Notice that
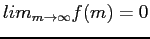 .
.
- Hence, contrary to Amdahl's law, a linear speed-up can be achieved for such a large-sized problem.
- It should be noted that in presenting the above scenario for solving the matrix vector multiplication problem, we have assumed that the memory size of each processor is large enough to store the maximum number of rows expected.
- This assumption amounts to us saying that with
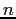 processors, the memory is
processors, the memory is 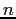 times larger.
times larger.
- Naturally, this argument is more applicable to message passing parallel architectures than it is to shared memory ones.
- The Gustafson-Barsis law makes use of this argument.
Cem Ozdogan
2010-12-27