- Multiplying the formula of Definition 2.9 by
 , we obtain the multiplicative rule, which enables us to calculate the probability that two events will both occur.
, we obtain the multiplicative rule, which enables us to calculate the probability that two events will both occur.
- Theorem 2.13:

- We can also write
- Example 2.35: Suppose that we have a fuse box containing 20 fuses, of which 5 are defective. If 2 fuses are selected at random and removed from the box in succession without replacing the first.
- What is the probability that both fuses are defective?
- Event
 : the first fuse is defective
: the first fuse is defective
- Event
 : the second fuse is defective. Hence,
: the second fuse is defective. Hence,
- Example 2.36: One bag contains 4 white balls and 3 black balls. A second bag contains 3 white balls and 5 black balls.
- One ball is drawn from the first bag and placed unseen in the second bag. What is the probability that a ball now drawn from the second bag is black?
- Solution: Let
 ,
,  , and
, and  represent, respectively, the drawing of a black ball from bag 1, a black ball from bag 2, and a white ball from bag 1.
represent, respectively, the drawing of a black ball from bag 1, a black ball from bag 2, and a white ball from bag 1.
Figure 2.6:
Tree diagram for Example 2.36.
|
|
- Theorem 2.14:

- Example 2.37: A small town has one fire engine and one ambulance available for emergencies.
- The probability that the fire engine is available when needed is 0.98,
- The probability that the ambulance is available when called is 0.92
- In the event of an injury resulting from a burning building, find the probability that both the ambulance and the fire engine will be available.
- Solution: Let
 and
and  represent the respective evens that the fire engine and the ambulance are available. Then
represent the respective evens that the fire engine and the ambulance are available. Then
- Example 2.38: Find the probability that
Figure 2.7:
An electrical system for Example 2.38.
|
|
- the entire system works
- the component
 does not work, given that the entire system works
does not work, given that the entire system works
- Solution:
- Independence is often easy to grasp intuitively.
- For example, if the occurrence of two events is governed by distinct and non-interacting physical processes, such events will turn out to be independent.
- On the other hand, independence is not easily visualized in terms of the sample space.
- A common fallacy (wrong idea) is that two events are independent if they are disjoint, but in fact the opposite is true:

- We note that
- (i)
- independent events are never mutually exclusive,
- (ii)
- two mutually exclusive events are always dependent.
- Theorem 2.15:

- Example 2.39: Three cards are drawn in succession without replacement. Find the probability that the event
 occurs, where
occurs, where
 : the first card is red ace
: the first card is red ace
 : the second card is a 10 or jack
: the second card is a 10 or jack
 : the third card is greater than 3 but less than 7
: the third card is greater than 3 but less than 7
- Solution:
- Independence of Several Events:

- Independence means that the occurrence or non-occurrence of any number of the events from that collection carries no information on the remaining events or their complements.
- Example: Independence of three events: If
 and
and  are independent,
are independent,
- Example: Consider two independent fair coin tosses, and the following events:
 =
=  toss is a head,
toss is a head,
 =
= 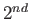 toss is a head,
toss is a head,
 = the two tosses have different results.
= the two tosses have different results.
- Pairwise independence does not imply independence.
 and
and  are independent, by definition.
are independent, by definition.
-
 and
and
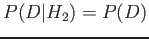
-

- Example: Consider two independent rolls of a fair die, and the following events:
 =
=  roll is 1, 2, or 3,
roll is 1, 2, or 3,  =
= 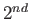 roll is 3, 4, or 5,
roll is 3, 4, or 5,  = the sum of the two rolls is 9.
= the sum of the two rolls is 9.
-
 is not enough for independence.
is not enough for independence.
Cem Ozdogan
2012-02-15









