Next: Joint Probability Distribution Up: Random Variables and Probability Previous: Discrete Probability Distributions Contents

A probability density function is constructed so that the area under its curve bounded by the ![]() axis is equal to 1.
axis is equal to 1.

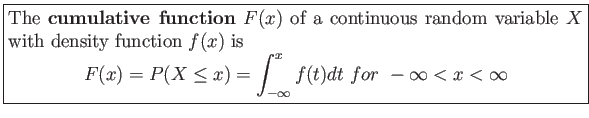
Example 3.12: For the density function of Example 3.6 find ![]() , and use it to evaluate
, and use it to evaluate
![]() .
.
For
![]()
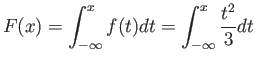


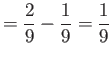
Cem Ozdogan 2012-02-15