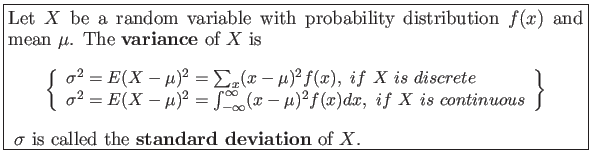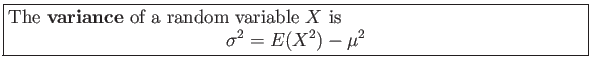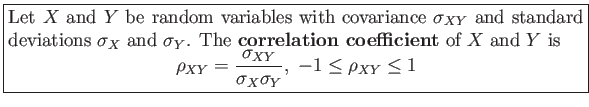- A mean does not give adequate description of the shape of a random variable (probability distribution).
- We need to characterize the variability (or dispersion) of the random variable
 in the distribution.
in the distribution.
Figure 4.1:
Distributions with equal means and unequal dispersions.
|
|
- Definition 4.3:
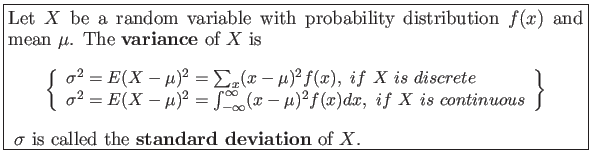
- Example 4.8:Let the random variable
 represent the number of automobiles that are used for official business purposes on any given workday.
represent the number of automobiles that are used for official business purposes on any given workday.
- The probability distribution for company A and B is as follows.
 |
1 |
2 |
3 |
 |
0.3 |
0.4 |
0.3 |
 |
0 |
1 |
2 |
3 |
4 |
 |
0.2 |
0.1 |
0.3 |
0.3 |
0.1 |
- Show that the variance of the probability distribution for company B is greater than that of company A.
- Solution:
- Theorem 4.2:
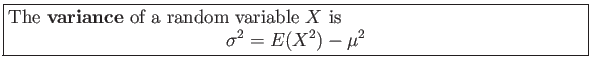
- Example 4.9: Let the random variable
 represent the number of defective parts for a machine when 3 parts are sampled from a production line and tested.
represent the number of defective parts for a machine when 3 parts are sampled from a production line and tested.
- Calculate
 using the following probability distribution.
using the following probability distribution.
 |
0 |
1 |
2 |
3 |
 |
0.51 |
0.38 |
0.10 |
0.01 |
- Solution:
- Theorem 4.3:

- Example 4.11: Calculate the variance of
 , where
, where  is a random variable with probability distribution.
is a random variable with probability distribution.
 |
0 |
1 |
2 |
3 |
 |
1/4 |
1/8 |
1/2 |
1/8 |
- Solution:
- Definition 4.4:

- The covariance between two random variables is a measurement of the nature of the association between the two.
- The sign of the covariance indicates whether the relationship between two dependent random variables is positive or negative.
- When
 and
and  are statistically independent, it can be shown that the covariance is zero.
are statistically independent, it can be shown that the covariance is zero.
- The converse, however, is not generally true. Two variables may have zero covariance and still not be statistically independent.
- The covariance only describe the linear relationship between two random variables.
- If a covariance between
 and
and  is zero,
is zero,  and
and  may have a nonlinear relationship, which means that they are not necessarily independent.
may have a nonlinear relationship, which means that they are not necessarily independent.
- Theorem 4.4:

- Definition 4.5:
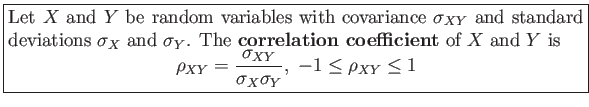
- Exact linear dependency:

Cem Ozdogan
2012-02-15