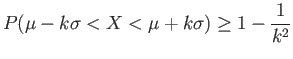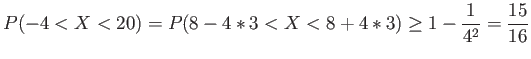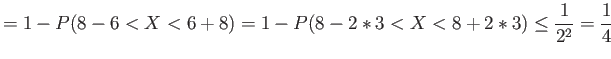- If a random variable has a small variance or standard deviation, we would expect most of the values to be grouped around the mean
- A large variance indicates a greater variability, so the area of distribution should be spread out more.
Figure 4.2:
Variability of continuous observations about the mean.
|
|
Figure 4.3:
Variability of discrete observations about the: mean.
|
|
- Theorem 4.11:

- Example 4.22: A random variable
 has a mean
has a mean 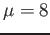 , a variance
, a variance
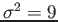 , and an unknown probability distribution. Find
, and an unknown probability distribution. Find
-
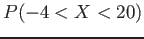
-

- The Chebyshev inequality is a useful tool as well as a relation that connects the variance of a distribution with the intuitive notation of dispersion in a distribution.
- For any population or sample, this provides that the minimum probability of the data within
 from the mean
from the mean  is
is
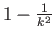 .
.
- The use of Chebyshev's theorem;
- holds for any distribution of observations
- gives a lower bound only
- is suitable to situations where the form of the distribution is unknown (a distribution-free result)
Cem Ozdogan
2012-02-15