- Random samples are selected to elicit information about the unknown population parameters.
- Some important statistics:
- sample mean
- sample variance
- Definition 8.4:

- Say
 is a function of the observed values in the random sample.
is a function of the observed values in the random sample.
- We would expect
 to vary somewhat from sample to sample.
to vary somewhat from sample to sample.
- That is a value of a random variable
 , called a statistic.
, called a statistic.
- Definition 8.5:
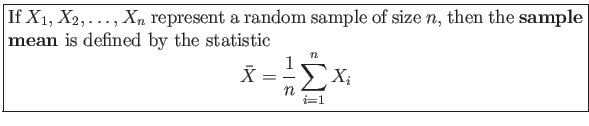
- The mean, median, and mode are the most commonly used statistics for measuring the central tendency.
- The computed value of
 for a given sample is denoted by
for a given sample is denoted by  .
.
- Sample mean is not the same thing as the mean of a random variable but they are very closely related.
- Sample mode is the observation value that occurs the most number of times in a sample.
- Sample median is the middle value of a sample after sorting.
- Definition 8.6:

- The computed value of
 for a given sample is denoted by
for a given sample is denoted by 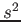 .
.
- Again this is very related to the standard deviation of a random variable but is not the same thing.
- Example 8.1: A comparison of coffee prices at 4 randomly selected grocery stores in San Diego showed increases from the
previous month of 12, 15, 17, and 20 cents for a 1-pound bag.
- Find the variance of this random sample of price increases.
- Solution:
- Theorem 8.1
![\fbox{\parbox{5in}{
If $S^2$ is the variance of a random sample of size $n$, we...
...n\sum_{i=1}^n X_i^2-\left( \sum_{i=1}^n X_i\right)^2\right]
\end{displaymath}}}](img887.png)
- Definition 8.7:

- Example 8.2: Find the variance of the data 3, 4, 5, 6, 6, and 7, representing the number of trout caught by a random sample of 6 fishermen.
- Solution:
Cem Ozdogan
2012-02-15

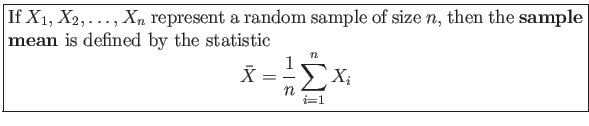



![\fbox{\parbox{5in}{
If $S^2$ is the variance of a random sample of size $n$, we...
...n\sum_{i=1}^n X_i^2-\left( \sum_{i=1}^n X_i\right)^2\right]
\end{displaymath}}}](img887.png)



