Sample Space

• Definition: (Probability theory) The mathematical study of randomness or mechanism of chance.
• In the study of statistics, we are concerned with the presentation and interpretation of chance outcomes.
• The outcome will depend on chance and, thus, cannot be predicted with certainty.
• Any recording of information, whether it be numerical or categorical, is referred to observation.
  • the number of accidents in one month: 2, 0, 1, 2.
  • the category that an inspected item belongs to: D, N, D, N, N.
• Experiment: any process that generates (or observe) a set of data.
  • E.g., tossing of a coin, two possible outcomes, heads and tails
  • In a statistical experiment, the data are subject to uncertainty.

• Definition 2.1: The set of possible outcomes of a statistical experiment is called the sample space,represented by $S$.
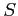• Each outcome in a sample space is called
  • an element,
  • a member of the sample space, or
  • a sample point.
• If the sample space has a finite number of elements, we may list the members.
• If the sample space has a large or infinite number of elements, we describe it by a statement or rule.
• Example 2.1.
  • Tossing a coin: $S = {H, T}$
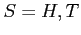
  • Tossing a die:
    • $S_1=\{1, 2, 3, 4, 5, 6\}$
    • $S_2= \{even, odd\}$
• A tree diagram can be used to list the elements of the sample space systematically.

• Example 2.2. Flip a coin first. If a head occurs, flip it again; otherwise, toss a die.
  • $S = \{HH, HT, T1, T2, T3,T4, T5, T6\}$

Figure 1: Tree diagram for Example 2.2.

• Example 2.3. Three items are selected at random from a process.
  • $S = \{DDD, DDN, DND, DNN, NDD, NDN, NND, NNN\}$

Figure 2: Tree diagram for Example 2.3.

• The rule method. The rule method has practical advantages, particularly for the many experiments where a listing becomes a tedious chore.
  • $S = \{x \vert~ x~is~ a~ city~ with~ population~ over~ 1~ million\}$.
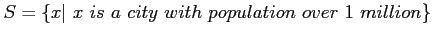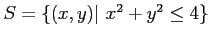  • $S = \{ (x,y) \vert~ x^2+y^2 \leq 4\}$, the set of all points 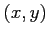$(x,y)$ on the boundary or the interior of a circle of radius 2 with center at the origin.