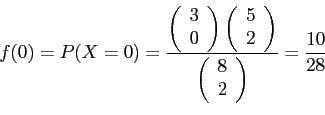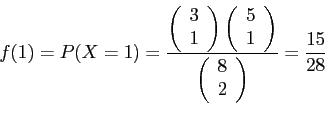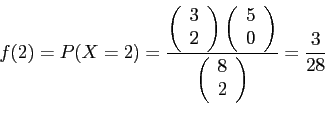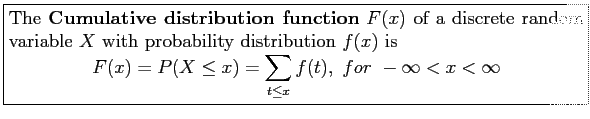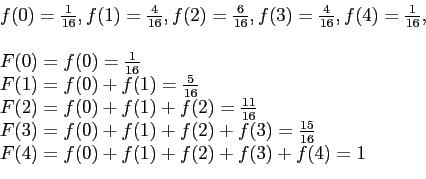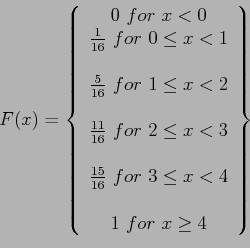Discrete Probability Distributions

• A discrete random variable assumes each of its values with a certain probability.
• Frequently, it is convenient to represent all the probabilities of a random variable $X$ by a formula;
  $$f(x)=P(X=x),~~f(3)=P(X=3)$$

• Definition 3.4:
  
• The probability distribution of a discrete random variable can be presented in the form of a mathematical formula, a table, or a graph- probability histogram or barchart.

Example: Let $X$ be the random variable: number of heads in 3 tosses of a fair coin.

Sample Space	$x$
TTT	0
TTH	1
THT	1
THH	2
HTT	1
HTH	2
HHT	2
HHH	3

 
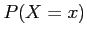$P(X=x)$: Probability that outcome is a specific $x$ value.

x	0	1	2	3
P(X=x)	$\frac{1}{8}$	$\frac{3}{8}$	$\frac{3}{8}$	$\frac{1}{8}$

• Example 3.8: A shipment of 8 similar microcomputers to a retail outlet contains 3 that are defective.
• If a school make a random purchase of 2 of these computers.
• Find the probability distribution for the number of defectives.

  x	0	1	2
  f(x)	$\frac{10}{28}$	$\frac{15}{28}$	$\frac{3}{28}$

$$f(0)=P(X=0)=\frac{ \left( \begin{array}{c} 3\\ 0\\ \end... ...\begin{array}{c} 8\\ 2\\ \end{array}\right)}=\frac{10}{28}$$

$$f(1)=P(X=1)=\frac{ \left( \begin{array}{c} 3\\ 1\\ \end... ...\begin{array}{c} 8\\ 2\\ \end{array}\right)}=\frac{15}{28}$$

$$f(2)=P(X=2)=\frac{ \left( \begin{array}{c} 3\\ 2\\ \end... ... \begin{array}{c} 8\\ 2\\ \end{array}\right)}=\frac{3}{28}$$

• Definition 3.5:
  
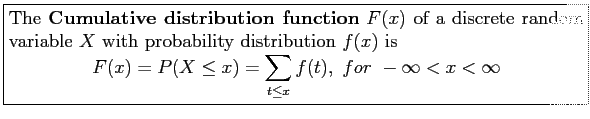
• Example 3.10: Find the cumulative distribution of the random variable $X$ in Example 3.9.

$$\begin{array}{l} f(0)=\frac{1}{16},f(1)=\frac{4}{16},f(2)=\... ...frac{15}{16}\\ F(4)=f(0)+f(1)+f(2)+f(3)+f(4)=1\\ \end{array}$$

$$F(x)=\left\lbrace \begin{array}{c} 0 ~ for~ x< 0\\ \frac... ...q x < 4 \\ \\ 1~ for~ x \geq 4 \\ \end{array}\right\rbrace$$

Figure 1: Bar chart and probability histogram

Figure 2: Discrete cumulative distribution.

[