- Deadlocks can be described more precisely in terms of a directed graph called a system resource-allocation graph.
- This graph consists of a set of vertices
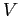 and a set of edges
and a set of edges 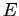 .
.
- The set of vertices
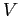 is partitioned into two different types of nodes:
is partitioned into two different types of nodes: 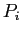 s and
s and 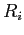 s.
s.
- A directed edge from process
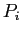 to resource type
to resource type 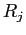 is denoted by
is denoted by
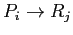 ; it signifies that process
; it signifies that process 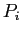 has requested an instance of resource type
has requested an instance of resource type 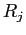 and is currently waiting for that resource (request edge).
and is currently waiting for that resource (request edge).
- A directed edge from resource type
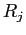 to process
to process 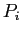 is denoted by
is denoted by
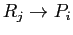 ; it signifies that an instance of resource type
; it signifies that an instance of resource type 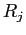 has been allocated to process
has been allocated to process 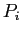 (assignment edge).
(assignment edge).
- Pictorially, each process
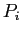 is represented as a circle and each resource type
is represented as a circle and each resource type 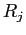 as a rectangle.
as a rectangle.
Figure 7.4:
Resource allocation graphs. (a) Holding a resource. (b) Requesting a resource. (c) Deadlock.
|
|
- An arc from a resource node (square) to a process node (circle) means that the resource has previously been requested by, granted to, and is currently held by that process (see Fig. 7.4).
- Since resource type
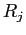 may have more than one instance, each such instance is represented as a dot within the rectangle.
may have more than one instance, each such instance is represented as a dot within the rectangle.
Figure 7.5:
Left: Resource-allocation graph. Middle: Resource-allocation graph with a deadlock. Right: Resource-allocation graph with a cycle but no deadlock
|
|
- The resource-allocation graph shown in Fig. 7.5left depicts the following situation. The sets
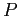 ,
, 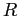 , and
, and 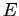 :
:
- Given the definition of a resource-allocation graph, it can be shown that, if the graph contains no cycles, then no process in the system is deadlocked. If the graph does contain a cycle, then a deadlock may exist.
- A cycle in the graph is a necessary but not a sufficient condition for the existence of deadlock with resource types of several instances. A knot must exist; a cycle with no non-cycle outgoing path from any involved node
- Suppose that process
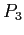 requests an instance of resource type
requests an instance of resource type 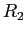 . Since no resource instance is currently available, a request edge
. Since no resource instance is currently available, a request edge
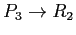 is is added to the graph (see Fig. 7.5middle).
is is added to the graph (see Fig. 7.5middle).
- At this point, two minimal cycles exist in the system.
- Now consider the resource-allocation graph in Fig. 7.5right.
- In this case, we also have a cycle. However, there is no deadlock.
- Observe that process
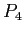 may release its instance of resource type
may release its instance of resource type 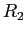 .
.
- That resource can then be allocated to
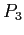 , breaking the cycle.
, breaking the cycle.
- In summary, if a resource-allocation graph does not have a cycle, then the system is not in a deadlocked state. If there is a cycle, then the system may or may not be in a deadlocked state.
- An example of resource allocation graphs (see Fig. 7.6);
Figure 7.6:
Resource Allocation Graphs. Lower; either 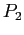 or
or 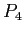 could relinquish (release) a resource allowing
could relinquish (release) a resource allowing 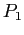 or
or 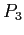 (which are currently blocked) to continue.
(which are currently blocked) to continue.
|
|
- Another example of how resource graphs can be used; three processes,
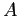 ,
, 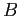 , and
, and 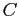 , and three resources
, and three resources 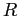 ,
, 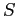 , and
, and 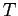 (see Fig. 7.7);.
(see Fig. 7.7);.
Figure 7.7:
An example of how deadlock occurs and how it can be avoided.
|
|
Cem Ozdogan
2011-02-14