- Another approach to free-space management is to link together all the free disk blocks, keeping a pointer to the first free block in a special location on the disk and caching it in memory.
- This first block contains a pointer to the next free disk block, and so on.
- In our earlier example (Section 11.5.1);
- We would keep a pointer to block 2 as the first free block.
- Block 2 would contain a pointer to block 3,
- which would point to block 4,
- which would point to block 5,
- which would point to block 8, and so on (see Fig. 11.16).
Figure 11.16:
Linked free-space list on disk.
|
|
- However, this scheme is not efficient; to traverse the list, we must read each block, which requires substantial I/O time. Fortunately, traversing the free list is not a frequent action.
- Usually, the OS simply needs a free block so that it can allocate that block to a file, so the first block in the free list is used.
- Keeping it in main memory;
- With a 1-KB block and a 32-bit (4 bytes) disk block number, each block on the free list holds the numbers of 255 free blocks. (1KB/32-bit=256; one slot is needed for the pointer to the next block. The number of blocks that could be addressed:
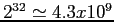 ).
).
- A 500-GB disk, which has about 488 million (
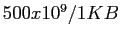 ) disk blocks . To store all these addresses at 255 per block requires about 1.9 million blocks (
) disk blocks . To store all these addresses at 255 per block requires about 1.9 million blocks (
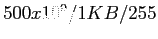 ). Generally, free blocks are used to hold the free list, so the storage is essentially free.
). Generally, free blocks are used to hold the free list, so the storage is essentially free.
- It is not surprising that the bitmap requires less space (60000 blocks), since it uses 1 bit per block, versus 32 bits in the linked list model. Only if the disk is nearly full (i.e., has few free blocks) will the linked list scheme require fewer blocks than the bitmap.
Figure 11.17:
(a) Storing the free list on a linked list. (b) A bitmap.
|
|
Cem Ozdogan
2011-02-14