- Location measures do not provide a proper summary of the nature of a data set.
- We can not make meaningful conclusion without considering sample variability. Example:
- Each data set contains two samples and the difference in the means is roughly the same.
- Data set B provides sharper distinction between two populations.
Figure 1.7:
Different data sets. Difference in the means is roughly the same.
|
|
- The simplest measures of sample variability is the sample range
 .
.
- The range can be very useful in statistical quality control.
- The question ``How far is each x from the mean?''
- The one that is used most often is the sample standard deviation.
- The sample variance, denoted by

- The sample standard deviation, denoted by
 , is the positive square root of
, is the positive square root of  , that is
, that is
- The sample variance is measured in squared units. The sample standard deviation is in linear units.
- For a bell-shaped distribution,
- within one standard deviation of the mean there will be approximately (empirically) 68% of the data;
- within two standard deviations of the mean there will be approximately 95% of the data;
- within three standard deviations of the mean there will be approximately 99.7% of the data.
- That is,
- This is a rule of thumb. Since the range
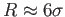 , the rule is also called the
, the rule is also called the 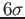 -rule.
-rule.
- An observation beyond (
 ) can be declared as an outlier.
) can be declared as an outlier.
- The quantity
 is called the degrees of freedom associated with the variance estimate.
is called the degrees of freedom associated with the variance estimate.
- It depicts the number of independent pieces of information available for computing variability. Only
 terms can vary freely.
terms can vary freely.
- In general,
- The computation of a sample variance does not involve
 independent squared deviations from the mean. For example,
independent squared deviations from the mean. For example,
- for the data set (5, 17, 6, 4), the sample mean is 8.
- The variance is
- The quantities inside parentheses sum to zero.
- Example 1.4. An engineer is interested in testing the ``bias'' in a pH meter. Data are collected on the meter by measuring the pH of a neutral substance (pH = 7.0). A sample of size 10 is taken with results given by
with 9 degrees of freedom.
- In statistical inference, we like to draw conclusions about characteristics of populations, called population parameters.
- Population mean and population variance are two important parameters.
- The sample variance is used to draw inferences about the population variance.
- The sample standard deviation and the sample mean are used to draw inferences about the population mean.
- In general, the variance is considered more in inferential theory, while the standard deviation is used more in applications.
Cem Ozdogan
2012-02-15

