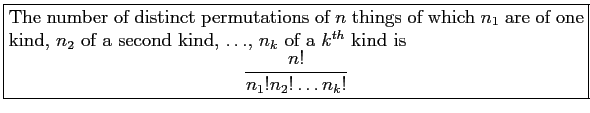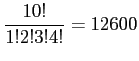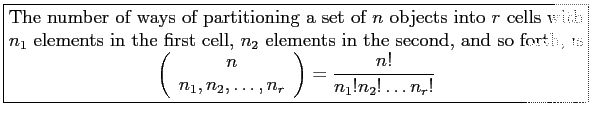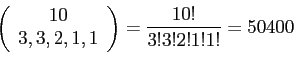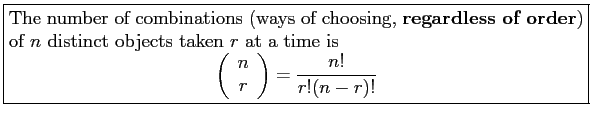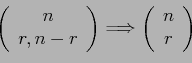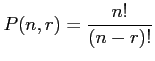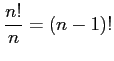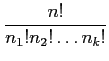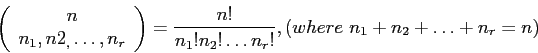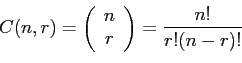- Combinatorics - counting rules in set theory. This provides the idea of the principles of enumeration, counting sample points in the sample space.
- When an experiment is performed, the statistician want to evaluate the chance associated with the occurrence of certain events.
- In many cases we can evaluate the probability by counting the number of points in the sample space.
- Theorem 2.1 (multiplication rule):

- The multiplication rule is the fundamental principle of counting sample points.
- Example 2.14: Home buyers are offered
- four exterior styling
- three floor plans
- Since
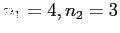 and , a buyer must choose from
and , a buyer must choose from
possible homes
Figure 4:
Tree diagram for Example 2.14.
|
|
- Theorem 2.2 (generalized multiplication rule):

- The multiplication rule can be extended to cover any number of operations.
- Example 2.16: How many even four-digit numbers can be formed from the digits 0, 1, 2, 5, 6, and 9 if each digit can be used only once?
- We consider the unit position by two parts, 0 or not 0.
- If the units position is 0
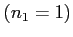 :
:
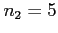 choices for the thousands positions,
choices for the thousands positions,
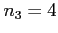 choices for the hundreds positions,
choices for the hundreds positions,
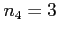 choices for the tens positions.
choices for the tens positions.
- a total of
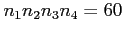 choices.
choices.
- If the units position is not 0
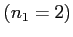 :
:
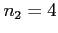 choices for the thousands positions,
choices for the thousands positions,
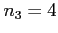 choices for the hundreds positions,
choices for the hundreds positions,
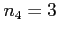 choices for the tens positions.
choices for the tens positions.
- a total of
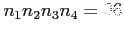 choices.
choices.
- The total number of even four-digit numbers is 60 + 96 = 156
- Permutation: Definition 2.7
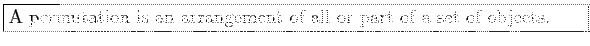
- An ordered arrangement of distinct objects. Consider the number of ways of filling
 boxes with
boxes with 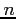 objects.
objects.
- Theorem 2.3:

- Theorem 2.4:

- Example 2.17: In one year, three awards (research, teaching, and service) will be given for a class of 25 graduate students in a statistics department.
- If each student can receive at most one award, how many possible selections are there?
- Since the awards are distinguishable, it is a permutation problem.
- The number of sample points is
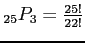
- Example 2.18: A president and a treasurer are to be chosen from a student club consisting of 50 people. How many different choices of officers are possible if
- there are no restrictions;
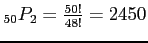
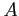 will serve only if he is president;
will serve only if he is president;
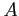 is selected as the president, which yields 49 possible outcomes; or
is selected as the president, which yields 49 possible outcomes; or
- Officers are selected from the remaining 49 people which has the number of choices
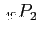
Therefore, the total number of choices is
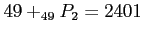 .
.
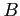 and
and 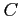 will serve together or not at all;
will serve together or not at all;
- The number of selections when
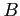 and
and 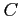 serve together is 2.
serve together is 2.
- The number of selections when both
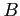 and
and 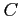 are not chosen is
are not chosen is 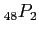
Therefore, the total number of choices in this situation is 2 + 2256 = 2258.
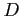 and
and 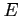 will not serve together;
will not serve together;
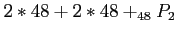
- The number of selections when
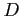 serves as officer but not
serves as officer but not 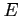 ,
,
- The number of selections when
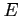 serves as officer but not
serves as officer but not 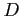
- The number of selections when both
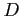 and
and 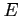 are not chosen
are not chosen
Therefore, the total number of choices is 2448. This problem also has another short solution:
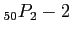 (since
(since 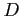 and
and 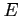 can only serve together in 2 ways).
can only serve together in 2 ways).
- Permutations are used when we are sampling without replacement and order matters.
- Theorem 2.5:
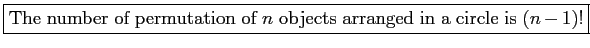
- Permutations that occur by arranging objects in a circular are called circular permutations.
- Two circular permutations are not considered different unless corresponding objects in the two arrangements are preceded or followed by a different objects as we proceed in a clockwise direction.
- Theorem 2.6:
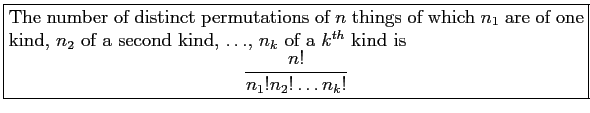
- Example 2.19: In a college football training session, the defensive coordinator needs to have 10 players standing in a row.
- Among these 10 players, there are 1 freshman, 2 sophomores, 4 juniors, and 3 seniors, respectively.
- How many different ways can they be arranged in a row if only their class level will be distinguished?
- Theorem 2.7:
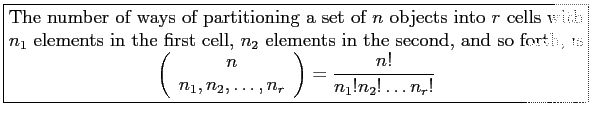
- The order of the elements within each cell is of no importance.
- The intersection of any two cells is the empty set and the union of all cells gives the original set.
- Example 2.22: How many different letter arrangements can be made from the letters in the word of STATISTICS?
- We have total 10 letters, while letters S and T appear 3 times each, letter I appears twice, and letters A and C
appear once each.
Cem Ozdogan
2010-03-01