- If all resources have only a single instance, then we can define a deadlock-detection algorithm that uses a variant of the resource-allocation graph, called a wait-for graph.
- This graph is obtained from the resource-allocation graph by removing the resource nodes and collapsing the appropriate edges.
- More precisely, an edge from
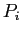 to
to 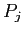 in a wait-for graph implies that process
in a wait-for graph implies that process 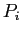 is waiting for process
is waiting for process 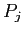 to release a resource that
to release a resource that 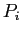 needs.
needs.
- For example, in Fig. 7.11, a resource-allocation graph and the corresponding wait-for graph are presented.
Figure 7.11:
(a) Resource-allocation graph. (b) Corresponding wait-for graph.
|
|
- As before, a deadlock exists in the system if and only if the wait-for graph contains a cycle.
- To detect deadlocks, the system needs to maintain the wait-for graph and periodically invoke an algorithm that searches for a cycle in the graph.
- If this graph contains one or more cycles (knots), a deadlock exists. Any process that is part of a cycle is deadlocked. If no cycles exist, the system is not deadlocked.
Figure 7.12:
(a) A resource graph. (b) A cycle extracted from (a).
|
|
- Consider a system with seven processes,
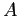 though
though 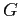 , and six resources,
, and six resources, 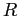 through
through 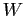 . The state of which resources are known and the the resource graph is given in Fig. 7.12. The question is: ``Is this system deadlocked, and if so, which processes are involved?''
. The state of which resources are known and the the resource graph is given in Fig. 7.12. The question is: ``Is this system deadlocked, and if so, which processes are involved?''
- From this cycle, we can see that processes
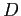 ,
, 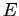 , and
, and 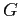 are all deadlocked. Processes
are all deadlocked. Processes 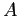 ,
, 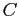 , and
, and 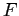 are not deadlocked because
are not deadlocked because 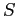 can be allocated to any one of them, which then finishes and returns it. Then the other two can take it in turn and also complete.
can be allocated to any one of them, which then finishes and returns it. Then the other two can take it in turn and also complete.
Cem Ozdogan
2011-02-14